Annuity Math Problems Examples

Therefore this is an ordinary general annuity. PV of annuity using intra-year discounting.

Pin On Math Angles

PVA 10 2000 PVIFA 62 102 PVA 10 2000 21065 Answer.

Annuity math problems examples. The present value of 25000 each year for 4 years at a 7 percent interest rate b. Let the equivalent annual rate be i. A regular annuity is simply an annuity where the first payment is made at the end of the period.

How much will you withdraw in this case. A 1 1 i1 n 1 the number of times interest is compounded per year. Distinguish between simple and.

P PV r 1 1rn. Now find the value of 1 invested at i per year after 1 year. Illustrate simple and general annuities2.

Suppose Mary wants to purchase an annuity that pays 1000month for the next 20 years. The present value of 152000 each year for 5 years at a 6 percent interest rate. For example if the compounding frequency isnt stated.

This is an example of an ordinary annuitylike those in previous lessons. If you make your deposits every quarter use quarterly compounding k 4. Alan wants to deposit 300 into a fund at the beginning of each month.

1000 1062517 10625 1000 Present Value of an Annuity Due. Let us see if we can determine the amount in the college fund and the interest earned. If he can earn 10 compounded interest monthly how much amount.

C cash flow per period i interest rate n number of payments beginaligned textFV_textOrdinaryAnnuity textC. FV Ordinary Annuity C 1 i n 1 i where. Future Value of an Annuity Due 3.

Notice that we can view the annuity as a series of three 100 lump sums or we can and will treat the cash flows as a package. Monthly payments of 500 where interest is 6a compounded monthly. Make sure to be consistent with the time period - if you use months you have to divide the annual interest rate by 12 and multiply the number of years by 12.

Using the formula A P 1 in find the value of 1 invested at 8a compounded quarterly after 1 year. FV 0 IY 5 CY 1 PMT 5000 PY 12 Years 15. The picture below show an example of a 3-period 100 regular annuity.

This is the annuity due formula. 5001084471-1084 500 FV 1889612 in the account in 7 years. Example 3 pg 416 Calculator.

Divide both sides by 1 1rn. Finan 36 Brief Discussion of Annuities A series of payments made at equal intervals of time is called an annu-ity. N is the number of periods.

If he can earn 10 compounded interest monthly how much amount will be there in the fund at the end of 6 years. If you need 30 000 in 10 years and you get an interest rate of 9 how much must you invest each of the next ten years. Suppose in Problem 1 above you deposited the payments on the last day of each year instead of the first so you would deposit your last payment on December 31 2028 then take all the money out the same day.

R is the interest rate per period as a decimal so 10 is 010. P is the value of each payment. If money earns an annual rate of 65 compounded quarterly how much would be.

P PV r 1 1rn. SIMPLE ANNUITY GRADE 11 GENERAL MATHEMATICS Q2In this video you will learn to1. PV is the Present Value of Annuity.

If you plan to save 100 annually for 5 years and the annual interest rate of 12 what is the future value. If you make your deposits every month use monthly compounding k 12. Find the present value of an annuity with periodic payments of 2000 for a period of 10 years at an interest rate of 6 discounted semiannually by factor formula.

The timeline for the deferred annuity appears below. P 1 1rn PV r. Calculating the Future Value of a Regular Annuity.

And we get this. In any problems that you see payment at the beginning of some time period this is the formula to use. 2 Suppose you invested 1000 per quarter over a 15 year period.

The interest rate on this annuity is 6. If you make your deposits every year use yearly compounding k 1. Multiply both sides by r.

Here the payment interval and the interest interval are the same 1 month. The deferred annuity has monthly payments at the end with an annual interest rate. We can find the value of the annuity right after the last deposit by using a geometric series with latexa_150latex and latexr10051005latex.

After the first deposit the value of the annuity will be 50. All the variables have the same meaning as the original annuity formula above. Common examples are house rents Examples include car loan home mortgage repayment.

Annuity Formula What Is Annuity Formula Examples

Calculating Present And Future Value Of Annuities

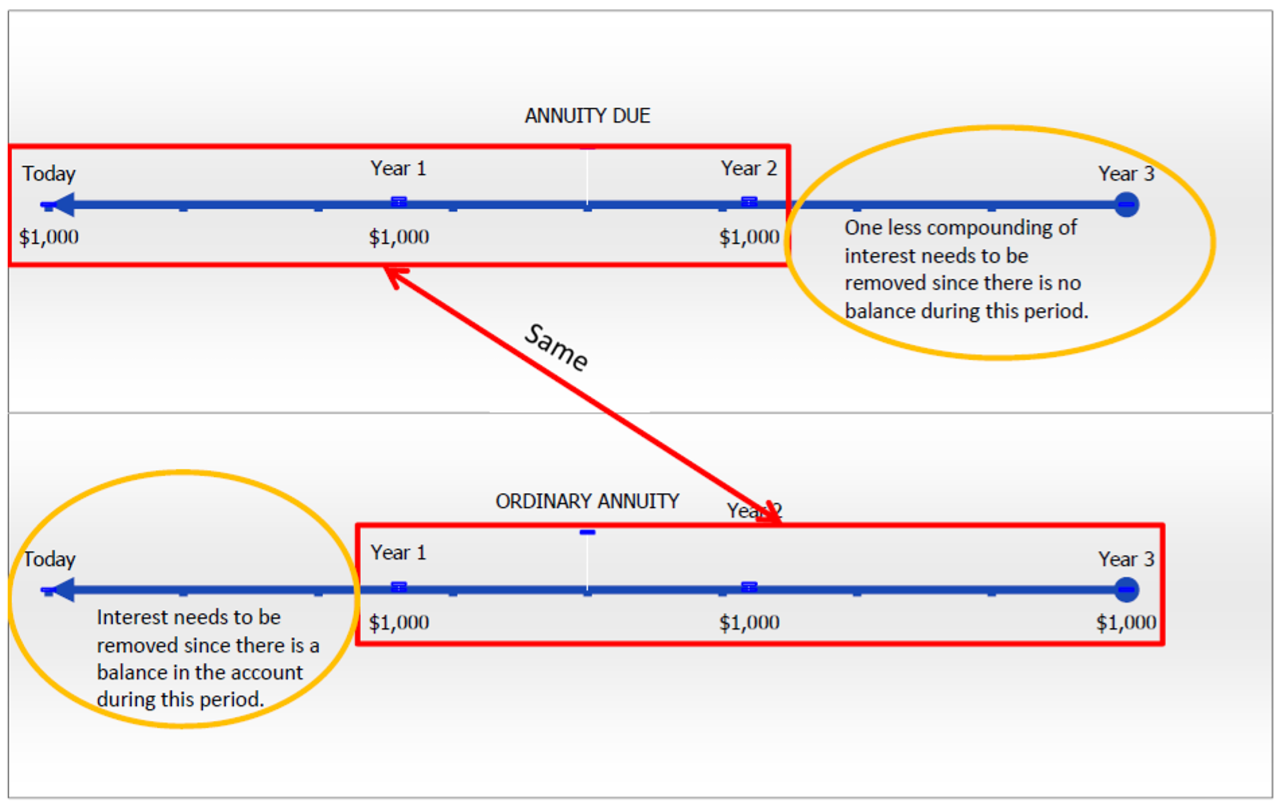
11 3 Present Value Of Annuities Mathematics Libretexts

Hsc Syjc Commerce Insurance And Annuity Chapter 3 Maths 2 Annuity Math Math 2

Calculating Present And Future Value Of Annuities

Calculating Present And Future Value Of Annuities

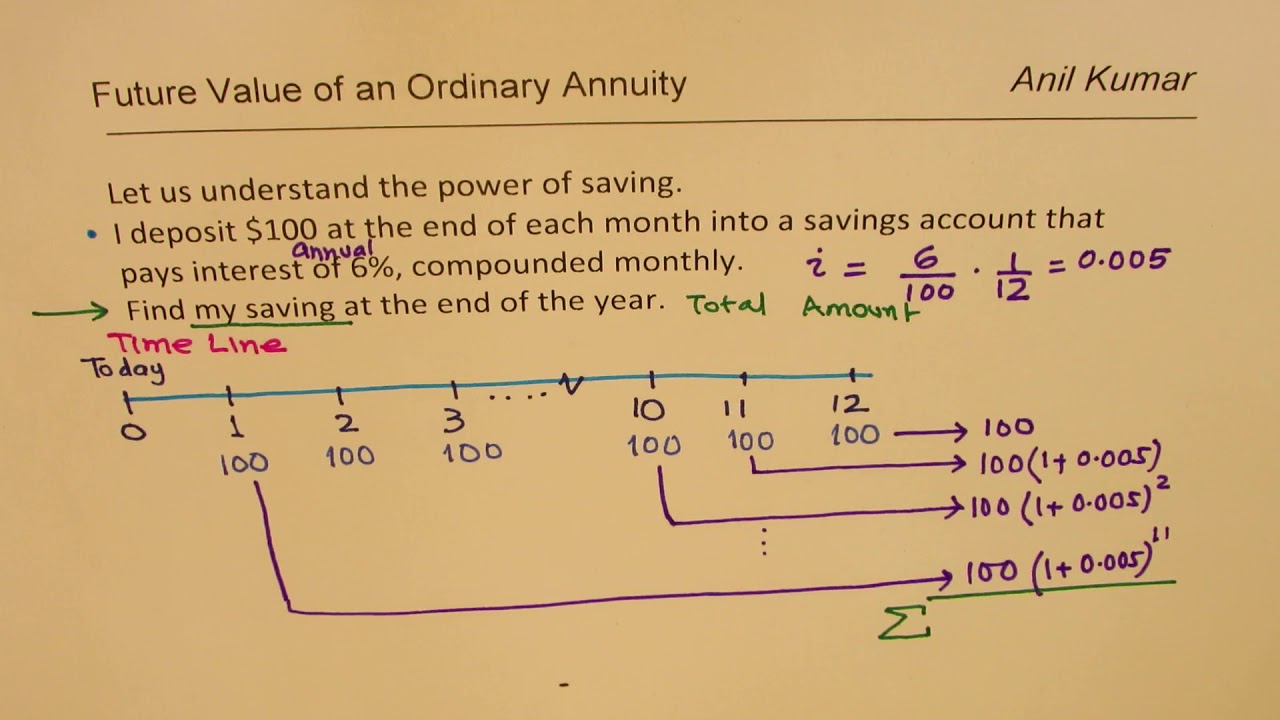
Future Value Of An Ordinary Annuity With Derived Formula Youtube

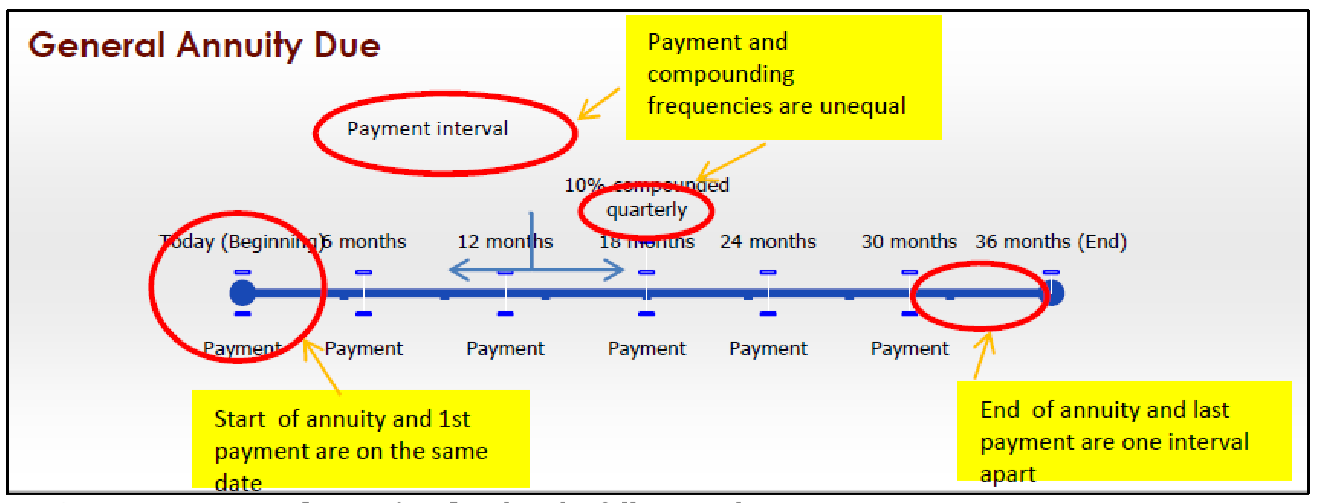
11 1 Fundamentals Of Annuities Mathematics Libretexts

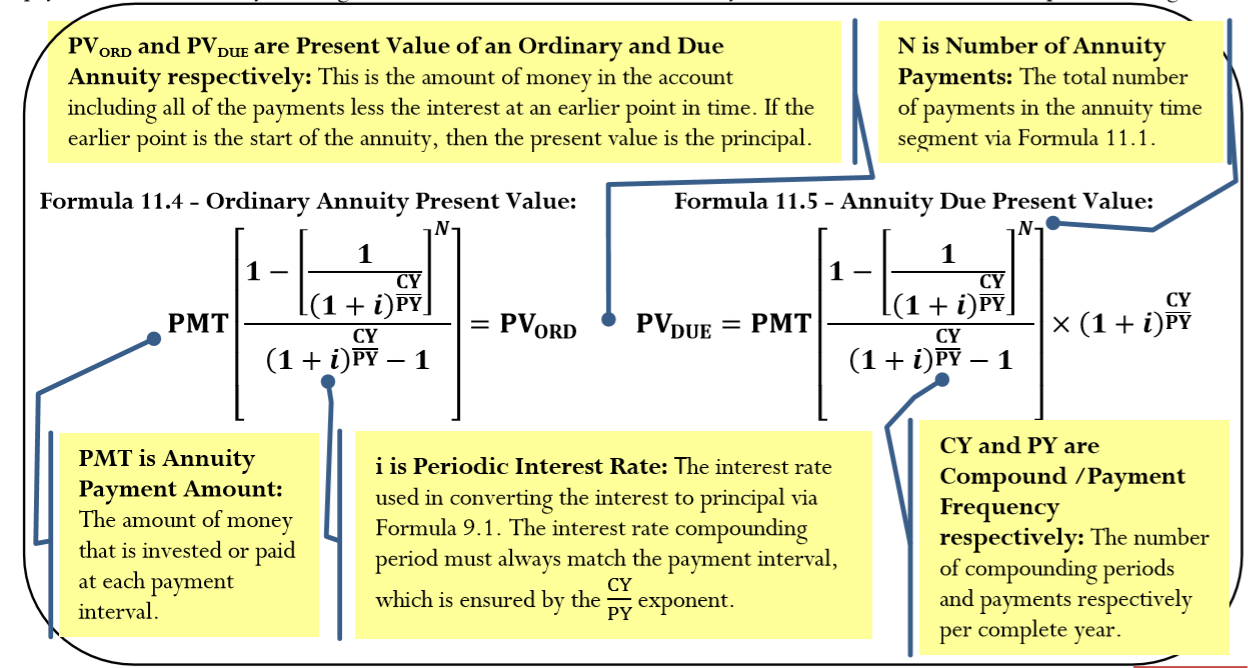
11 3 Present Value Of Annuities Mathematics Libretexts

How To Find The Value Of An Annuity Video Lesson Transcript Study Com

Determining The Value Of An Annuity Youtube

Pin On Math

Calculating Present And Future Value Of Annuities

Time Value Of Money Formulas Infographic Covering Perpetuity Growing Perpetuity Annuity Growing Annuity Annuity Time Value Of Money Annuity Formula Annuity

Time Value Of Money Financial Mathematics Icezen Time Value Of Money Accounting And Finance Finance

Annuity Formula Annuity Formula Annuity Economics Lessons

Determine The Required Savings To Reach A Financial Goal Financial Goals Finance Saving Annuity Formula

Pin On Knowledge Platter

Pv Function Excel Learning Microsoft Annuity Formula